Abstract
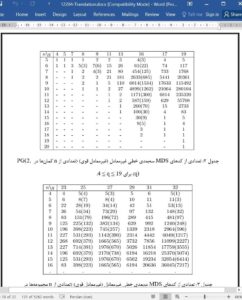
The number of (a) non-equivalent 2 and 3 dimensional MDS codes, (b) non-equivalent 3 dimensional complete MDS codes, (c) 3 dimensional MDS codes that can be described by classical arcs in PG(2, q), (d) arcs in regular hyperovals, and (e) 2 × n and 3 × n superregular matrices over GF(q) are established for q ≤ 19 and for a number of cases when 23 ≤ q ≤ 32. The equivalence classes over both PGL(k, q) and PΓL(k, q) are considered during the computations. Though, most of the results are reached by the help of a computer, also some general theoretical relations are formulated. A computational result of the paper is that there is no complete n-arc in PG(2, 31) for 23 ≤ n ≤ 30 and, consequently, the Main Conjecture for MDS Codes is true for arcs in up to 12 dimensional finite projective spaces of order 31, i.e., for MDS codes of up to 13 dimensions over GF(31).
Introduction
The aim of the present work is to determine the number of equivalence classes regarding three different equivalence relations and to build databases of k dimensional MDS codes over the finite fields GF(q) which contain one representant from each equivalence class. In the first phase of the project, we draw the limits for the range of these examinations at k ≤ 3 and q ≤ 32. As the databases become very huge when q advances towards 32, the aimed classification is impossible to carry out without using a computer. By performing exhaustive computer search, the problem is solved completely for 2 dimensional MDS codes until q ≤ 32 and for 3 dimensional MDS codes until q ≤ 19, it is solved partially for 3-dimensional MDS codes when 23 ≤ q ≤ 32.