Abstract
This paper is aimed at applying deep artificial neural networks for solving system of ordinary differential equations. We developed a vectorized algorithm and implemented using python code. We conducted different experiments for selecting better neural architecture. For the learning of the neural network, we utilized the adaptive moment minimization method. Finally, we compare the method with one of the traditional numerical methods-Runge–Kutta order four. We have shown that, the artificial neural network could provide better accuracy for smaller numbers of grid points.
1. Introduction
Deep neural network (DNN) has obtained great attention for solving engineering problems. System of ordinary differential equations (ODEs) that can model various physical phenomena could utilize the advantages of using the method. Though there are well established traditional numerical methods for solving systems of ODEs, they have their own advantages and disadvantages in-terms of accuracy, stability, convergence, computation time etc. One of the well known method is the fourth order Runge–Kutta method (RK4). It is among the finite difference methods well suited for non-stiff problems.
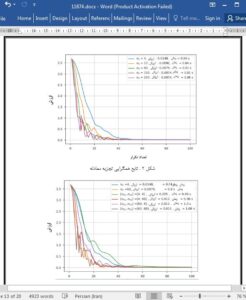
6. Conclusions and outlook
In this paper, we presented a vectorized algorithm for solving systems of ODE using DNN. We conducted different experiment using python code and simulated the result using graphs. We have obtained some insight on the nature of the architecture for the model. We have seen that for some specific problems we can obtain a required accuracy even for a single neuron in the hidden layer. More neuron size provides more accuracy, but more iteration for learning the parameters.