Abstract
Auxetic spacer fabrics are a novel kind of three-dimensional (3D) fabric structure with a negative Poisson’s ratio. They have found a number of applications in functional garments, protective pads and sportive shoes due to their unusual properties. In this paper, a study on deformation behaviors of 3D spacer fabrics that could be fabricated on a large scale is reported. Through experimental observations of deformation of a basic hexagonal unit at different tensile strains, two different geometrical models are proposed for the fabric structure when extended in the course direction and wale direction, respectively. Based on the geometrical models, two semi-empirical equations between the Poisson’s ratio and tensile strain are established for both tensile directions. The study shows that the established semi-empirical equations fit well with experimental results. Therefore, they could be used in the design and prediction of 3D auxetic spacer fabrics with different values of geometrical parameters.
Auxetic fabrics are a kind of textile structure with a negative Poisson’s ratio (PR).1,2 They laterally expand when stretched or laterally shrink when compressed. This unusual behavior makes them very interesting in many applications, such as functional garments, health care, protective clothing and so on, due to a number of fascinating properties, such as enhanced porosity under extension, excellent formability to curved surfaces, high energy absorption ability, etc.2
Conclusions
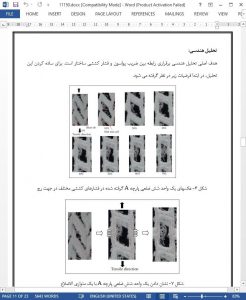
The deformation behaviors of 3D auxetic spacer fabric structure in both the course and wale directions were studied based on the experimental observations of a hexagonal unit and theoretical analysis of geometrical models proposed. The semi-empirical equation between the PR and tensile strain was established for each tensile direction. Some conclusions could be drawn from the study.
1. Due to the anisotropic behavior of the 3D auxetic structure, different geometrical models are needed for analyzing deformation behaviors of the structure in different tensile directions. While the deformation of the hexagonal unit in the course direction can be represented by deformation of a parallelogram, the deformation of the hexagonal unit in the wale direction always keeps in a hexagonal form.