Abstract
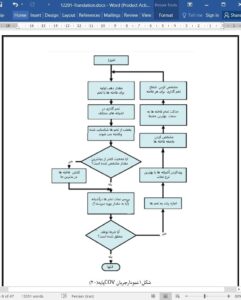
Cuckoo optimization algorithm (COA) is inspired from the special and exotic lifestyle of a bird family called the cuckoo and her amazing and unique behavior in egg laying and breeding. Just like any other population-based swarm intelligence metaheuristic algorithms, the basic COA starts with a set of randomly generated solutions called “habitats.” Actually, the habitats can be the current locations of either the mature cuckoos or their eggs. In an iterative manner, cuckoos lay their eggs around their habitats inside the other birds’ nests by mimicking their eggs’ color, pattern, and size, and this is a kind of parasitic brooding behavior. Some hosts may discriminate the strange eggs and throw them out while the others not. The survival competition between cuckoos and their hosts, and migration of cuckoos in swarm are two main underlying motivations to introduce the COA. In this paper, an adaptive cuckoo optimization algorithm named A-COA is proposed in which three novelties in egg-laying and migration phases are applied. These modifications have made the basic algorithm more efficient with faster convergence to solve continuous and discrete optimization problems. A comprehensive comparison study of A-COA versus not only the basic COA but also some other conventional metaheuristics like GA, PSO, ABC, and TLBO has been made on a variety of unimodal and multimodal numerical benchmark functions with different characteristics, and the results show an overall 25.85% of improvement in terms of performance with a faster convergence speed compared to the basic COA, where the statistical Wilcoxon rank-sum test certifies our conclusions. In addition, a discretized version of A-COA and its application to the multiprocessor task scheduling problem as a complex combinatorial optimization problem are investigated where the proposed A-COA is very competitive with not only the strongest conventional heuristics, for example, MCP, ETF, and DLS, but also the basic COA and the newly proposed ACO-based approach.
1 Introduction
Most of scientific, engineering and industrial problems can be formulated as a corresponding continuous or discrete objective function with some global optima and a large number of local minima/maxima around. Actually, such kinds of problems are NP-hard from the time complexity perspective, so that there are no exact algorithms to solve them in polynomial time budget. On this basis, using exact methods is impractical specially where the dimensionality of the problem at hand is high, and hence, metaheuristic algorithms, which have a significant potential as general problem solvers, to solve such kinds of problems have been receiving increasing attention in recent years. Such methods, which most of them are inspired from natural phenomena, are capable of finding at least suboptimal solutions in a significantly reduced time budget. Considering different factors, such methods can be discriminated into the different categories. Of them, two important ones introduced in the literature are evolutionary algorithms (EA) and swarm intelligence (SI) ones.
7 Conclusion
In this paper, an adaptive version of cuckoo optimization algorithm named A-COA with three novelties in the egglaying and migration phases was proposed. (1) The egglaying radius (ELR) was nonlinearly reduced over the iterations for faster convergence, inducing a better balance between exploration and exploitation, especially in the last iterations. (2) After egg-laying phase, those eggs laid in the same locations (with an e tolerance) are recognized and killed except one of them. While in the basic COA the epsilon coefficient was constant all over the execution, in the A-COA this coefficient was decreased linearly with the iterations. This idea lets compacter populations in the last iterations help with the exploitation and local search for getting exact final solutions. (3) In contrast to the basic COA in which the motion coefficient is constant during the algorithm execution, in the A-COA, we applied an adoptive motion coefficient for each cuckoo based on the cuckoo’s distance to the global best; i.e., the farer cuckoo would get higher coefficient to move forward. This idea, on the one hand, helped the farer cuckoos get trapped in the local minima having a big jump toward the global best and exiting off the stagnation while helping the convergence speed; on the other hand, it slowed down the speed of the nearer cuckoos for a better investigation around the global best in order to improve the accuracy as well as avoid premature convergence.