Abstract
We propose to solve the link prediction problem in graphs using a supervised matrix factorization approach. The model learns latent features from the topological structure of a (possibly directed) graph, and is shown to make better predictions than popular unsupervised scores. We show how these latent features may be combined with optional explicit features for nodes or edges, which yields better performance than using either type of feature exclusively. Finally, we propose a novel approach to address the class imbalance problem which is common in link prediction by directly optimizing for a ranking loss. Our model is optimized with stochastic gradient descent and scales to large graphs. Results on several datasets show the efficacy of our approach.
1 The Link Prediction Problem
Link prediction is the problem of predicting the presence or absence of edges between nodes of a graph. There are two types of link prediction: (i) structural, where the input is a partially observed graph, and we wish to predict the status of edges for unobserved pairs of nodes, and (ii) temporal, where we have a sequence of fully observed graphs at various time steps as input, and our goal is to predict the graph state at the next time step. Both problems have important practical applications, such as predicting interactions between pairs of proteins and recommending friends in social networks respectively. This document will focus on the structural link prediction problem, and henceforth, we will use the term “link prediction” to refer to the structural version of the problem.
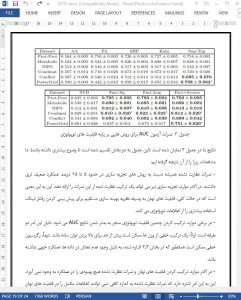
6 Conclusion
In the paper, we proposed a model that extends matrix factorization to solve structural link prediction problems in (possibly directed) graphs. Our model combines latent features with optional explicit features for nodes and edges in the graph. The model is trained with a ranking loss to overcome the imbalance problem that is common in link prediction datasets. Training is performed using stochastic gradient descent, and so the model scales to large graphs. Empirically, we find that the latent feature approach significantly outperforms popular unsupervised scores, such as Adamic-Adar and Katz. We find that it is possible to learn useful latent features on top of explicit features, which can give better performance than either model individually. Finally, we observe that optimizing with a ranking loss can improve AUC performance by around 10% over a standard regression loss. Overall, on six datasets from widely different domains, some possessing side information and others not, our proposed method (FactBLR-Rank from Table 5 on datasets with side information, Fact-Rank on the others) has equal or better AUC performance (within statistical error) than previously proposed methods.