Abstract
Boussinesq’s problem for the indentation of an isotropic, homogeneous elastic halfspace by a rigid circular punch constitutes a seminal problem in the theory of contact mechanics as does Mindlin’s problem for the action of a concentrated force at the interior of an isotropic, homogeneous elastic halfspace. The combined action of the surface indentation in the presence of the interior loading is referred to as the Boussinesq–Mindlin problem, which has important applications in the area of geomechanics. The Boussinesq–Mindlin problem, which represents a self-stressing loading configuration, serves as a useful model for interpreting the mechanics of indentation of geologic media for purposes of estimating their bulk elasticity properties. In this paper, the analysis of the problem is extended to include an exponential variation in the linear elastic shear modulus of the halfspace region.
1. Introduction
The problem of the indentation of an isotropic elastic halfspace by a rigid circular indenter with a frictionless flat base is a seminal problem in contact mechanics that has applications in a variety of areas in the engineering sciences ranging from materials engineering to the earth sciences. The solution to the problem was obtained by Boussinesq [1] using results of potential theory, and subsequently it was solved by Harding and Sneddon [2] using the theory of dual integral equations. Since these developments, the area of contact mechanics has been extensively and exhaustively examined by researchers to the point that an extensive list of articles cannot be documented within the context of a regular article. Some of the landmark studies related to elastostatic contact mechanics in general are due to Hertz [3], Shtaerman [4], Galin [5], Ufliand [6] and Lur’e [7], and references to studies in contact mechanics are also given by Korenev [8], Ling [9], Goodman [10], Selvadurai [11–14], Gladwell [15], Johnson [16], Curnier [17] and Selvadurai and Atluri [18].
7. Concluding remarks
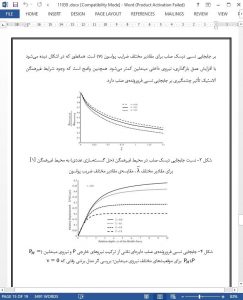
The present work provides the solutions for the case of a Cable Jacking Test related to an isotropic non-homogeneous elastic halfspace region where the linear elastic shear modulus varies exponentially with distance normal to the indented surface. The resulting integral equations, however, cannot be solved using the conventional analytical procedures that have been used to examine contact problems. In this paper, a discretization procedure [11,53,61,62] is used to develop an approximate solution. The results developed using this technique are presented to examine the effect of the Poisson’s ratio, variation of shear modulus with depth and the depth of location of the internal Mindlin-type point load. It should be noted that the basic objective of the Cable Jacking Test is to interpret the geomechanical properties of the tested rock mass through an interpretation of the load-displacement relationship for the test plate.