ترجمه مقاله یک جستجوی ممنوعه (تابو) کارآمد برای حل مسئله تخصیص محل هاب مجزا با ظرفیت نامحدود - نشریه الزویر

قیمت خرید این محصول

۴۱,۰۰۰ تومان

دانلود رایگان نمونه دانلود مقاله انگلیسی

عنوان فارسی

یک جستجوی ممنوعه (تابو) کارآمد برای حل مسئله تخصیص محل هاب مجزا با ظرفیت نامحدود

عنوان انگلیسی

An efficient tabu search for solving the uncapacitated single allocation hub location problem

صفحات مقاله فارسی

30

صفحات مقاله انگلیسی

11

سال انتشار

2016

رفرنس

دارای رفرنس در داخل متن و انتهای مقاله

نشریه

الزویر - Elsevier

فرمت مقاله انگلیسی

PDF

فرمت ترجمه مقاله

pdf و ورد تایپ شده با قابلیت ویرایش

فونت ترجمه مقاله

بی نازنین

سایز ترجمه مقاله

14

نوع مقاله

ISI

نوع نگارش

مقالات پژوهشی (تحقیقاتی)

نوع ارائه مقاله

ژورنال

پایگاه

اسکوپوس

ایمپکت فاکتور(IF) مجله

4.485 در سال 2019

شاخص H_index مجله

111 در سال 2020

شاخص SJR مجله

1.334 در سال 2019

شناسه ISSN مجله

0360-8352

شاخص Q یا Quartile (چارک)

Q1 در سال 2019

کد محصول

10734

وضعیت ترجمه عناوین تصاویر و جداول

ترجمه شده است ✓

وضعیت ترجمه متون داخل تصاویر و جداول

تصویر ترجمه شده است ✓ جداول ترجمه نشده است ☓

وضعیت ترجمه منابع داخل متن

ترجمه شده است ✓

وضعیت فرمولها و محاسبات در فایل ترجمه

به صورت عکس، درج شده است ✓

ضمیمه

ندارد ☓

بیس

نیست ☓

مدل مفهومی

ندارد ☓

پرسشنامه

ندارد ☓

متغیر

ندارد ☓

رفرنس در ترجمه

ر داخل متن و انتهای مقاله درج شده است

رشته و گرایش های مرتبط با این مقاله

مهندسی فناوری اطلاعات، کامپیوتر، شبکه های کامپیوتری، سامانه های شبکه ای، مهندسی الگوریتم ها و محاسبات

مجله

مهندسی صنایع و کامپیوتر - Computers & Industrial Engineering

دانشگاه

دانشکده علوم ریاضی، گروه ریاضی کاربردی، دانشگاه فردوسی مشهد، ایران

کلمات کلیدی

مسائل تخصیص هاب، تخصیص محل هاب مجزا با ظرفیت نامحدود، مسئله، جستجوی ممنوعه، فرااکتشافی

کلمات کلیدی انگلیسی

Hub location problems - Uncapacitated single allocation hub location problem - Tabu search - Metaheuristic

doi یا شناسه دیجیتال

https://doi.org/10.1016/j.cie.2015.12.028

۰.۰ (بدون امتیاز)

امتیاز دهید

فهرست مطالب

چکیده
1-مقدمه
2- فرمولاسیون ترکیبی
3- جستجوی تابو برای USAHLP (TSUSAHLP)
3-1- فضای راه حل
3-2- راه حل اولیه
3-3- انتقالهای محتمل
3-4- ایجاد یک تخصیص امکانپذیر برای انتقال موقعیت
3-5- حافظه کوتاه مدت
3-6- حافظه طولانی مدت
3-7- TSUSAHLP
4- بروزرسانی مقدار تابع هدف
5- آزمایشات محاسبه¬ای
5-1- مجموعه داده CAB
5-2- مجموعه داده AP
5-3- مجموعه داده AP تغییر یافته
5-4- نمونه¬های بزرگ براساس مجموعه داده AP
6- نتیجه¬گیریها

تصاویر فایل ورد ترجمه مقاله (جهت بزرگنمایی روی عکس کلیک نمایید)

نمونه چکیده متن اصلی انگلیسی

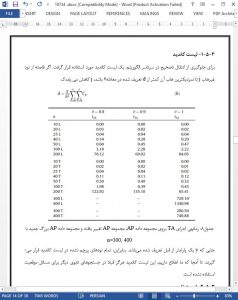
Abstract

We here propose an efficient tabu search (TS) for solving the uncapacitated single allocation hub location problem. To decrease the computational time, in the proposed tabu search, some new tabu rules are considered. Also, to compute the changes in the objective function’s value in each move, some new results are given. The performance of the proposed tabu search is compared with a recently proposed tabu search (Silva & Cunha, 2009) on all standard ORLIB instances (CAB and AP data sets), modified AP data set and finally on four large instances with 300 and 400 nodes proposed by Silva and Cunha. The numerical experiments show that the proposed tabu search can find all optimal solutions of CAB data and the best known solution of other standard test problems in less computational time than Silva and Cunha’s tabu search. Also, the proposed tabu search can improve the best known solutions for some standard test problems.

1. Introduction

Hub location problems are widely applied in postal networks (Ebery, Krishnamoorthy, Ernst, & Boland, 2000; Kuby & Gray, 1993), airlines (Aykin, 1995; Bania, Bauer, & Zlatoper, 1998; Karimi & Bashiri, 2011; Yang, 2009), telecommunication networks (Carello, Croce, Ghirardi, & Tadel, 2004; Helme & Magnanti, 1989; Kim & OKelly, 2009), transportation systems (Aversa, Botter, Haralambides, & Yoshizaki, 2005; Cunha & Silva, 2007; Don, Harit, English, & Whisker, 1995), emergency services (Campbell, 1994; Hakimi, 1964), etc. Generally, hub location problems are used in systems which have many origins and destinations, and direct link between each o–d1 is impossible or expensive. In these location–allocation problems, flows consolidate at hub nodes. Thus, all transportation become possible through hubs and also, costs are reduced because of the economical advantages of the scale.

In hub location problems, usually, hubs are fully interconnected, transferring between hubs includes a discount factor, and direct links between non-hub nodes are not allowed. In addition, in most of hub location problems, hubs are a subset of discrete nodes, however there are some researches on continuous hub location problems (see Aykin & Brown, 1992; Campbell, 1990; OKelly, 1992).

6. Conclusions

We here proposed an efficient tabu search (TS) for solving the uncapacitated single allocation hub location problem (USAHLP). To decrease the computational time, in the proposed tabu search, some new tabu rules were considered. Also, to compute the changes in the objective function’s value in each move, some new results were given. The performance of the proposed tabu search was compared with recently proposed approaches on all standard ORLIB instances (CAB and AP data sets), modified AP data set and finally on four large instances with 300 and 400 nodes proposed by Silva and Cunha. The numerical experiments showed that the proposed algorithm obtained the optimal solution for instances which optimal solutions are proven. Furthermore, our proposed tabu search obtained the best known solution found in the literature or surpass them in a very short computational time. It is notable that our proposed tabu search obtained the same solution in each run against other methods proposed for USAHLP. Our proposed TS outperforms the recently proposed TS (Silva & Cunha, 2009) in both solution values and computational times.

نمونه چکیده ترجمه متن فارسی

چکیده
در اینجا ما یک جستجوی ممنوعه (TS) کارآمد برای حل مسئله تخصیص محل (موقعیت) هاب مجزا با ظرفیت نامحدود پیشنهاد می کنیم.. برای کاهش زمان محاسبه ای در جستجوی تابو پیشنهادی، برخی قوانین جدید تابو در نظر گرفته شده اند. همچنین، برای محاسبه تغییرات در مقدار تابع هدف در هر انتقال، برخی نتایج جدید ارائه شده اند. عملکرد جستجوی ممنوعه پیشنهادی با یک جستجوی تابو اخیرا پیشنهاد شده توسط سیلوا و کانها (2009) بر روی تمام نمونه های ORLIB استاندارد (مجموعه داده های CAB و AP)، مجموعه داده های تغییر یافته AP و در نهایت بر روی چهار نمونه بزرگ با 300 و 400 نود پیشنهادی توسط سیلوا و کانها مقایسه شده است. آزمایشات عددی نشان می دهند که که جستجوی تابوی پیشنهادی می تواند تمام راه حلهای بهینه داده های CAB و مشهورترین راه حل مسائل آزمون استاندارد دیگر را در زمان محاسبه ای کم نسبت به جستجوی تابوی سیلوا و کانها پیدا کند. همچنین، جستجوی تابوی پیشنهادی میتواند بهترین راه حلها برای برخی مسائل آزمون استاندارد را بهبود بخشد.
1-مقدمه
مسائل تخصیص هاب به طور گسترده در شبکه های پستی (ابری و همکاران، 2000؛ . . .)، خطوط هوایی (آیکین، 1995؛ . . .)، شبکه های ارتباط از راه دور (کارلو و همکاران، 2004؛ . . .)، سیستم های حمل و نقل (آورسا و همکاران، 2005؛ . . .)، خدمات اورژانس (کمپل، 1994؛ . . .) و غیره به کار گرفته شده اند. به طور کلی، مسائل تخصیص هاب در سیستم هایی استفاده شده اند که دارای مبدا و مقصدهای بسیاری می باشند و لینک مستقیم بین هر o-d (مبدا-مقصد) غیرمحتمل یا هزینه بر می باشد. در این مسائل تخصیص محل (موقعیت)، جریانها در نودهای هاب تحکیم شده اند. بنابراین، تمام حمل و نقل از طریق هابها محتمل می باشد و همچنین هزینه ها به دلیل مزایای اقتصادی مقیاس کاهش یافته اند.
در مسائل تخصیص هاب، معمولا هابها به طور کامل دارای ارتباط متقابل می باشند، اتصال بین هاب شامل یک عامل تنزیل می باشد و لینکهای مستقیم بین نودهای غیرهاب مجاز نمی باشد. به علاوه، در اغلب مسائل تخصیص هاب، هاب یک زیرمجموعه از نودهای گسسته می باشد. به هر حال، برخی تحقیقات بر روی مسائل تخصیص هاب پیوسته نیز وجود دارند (آیکین و براون، 1992؛ کمپل، 1990؛ اوکلی، 1992 را ببینید).
6- نتیجه گیری ها
در اینجا، ما یک جستجوی ممنوعه (TS) کارآمد برای حل مسئله تخصیص محل هاب مجزا با ظرفیت نامحدود (USAHLP ) پیشنهاد کردیم. برای کاهش زمان محاسبه ای، در جستجوی ممنوعه پیشنهادی، برخی قوانین تابوی جدید در نظر گرفته شدند. همچنین برای محاسبه تغییرات در مقدار تابع هدف در هر انتقال، برخی نتایج جدید ارائه شدند. عملکرد جستجوی تابوی پیشنهادی با رویکردهای اخیرا پیشنهاد شده بروی تمام نمونه های ORLIB استاندارد (مجموعه داده های CAB و AP)، مجموعه داده AP تغییر یافته و در نهایت بر روی چهار نمونه بزرگ با 300 و 400 نود پیشنهاد شده توسط یلوا و کانها مقایسه شد. آزمایشات عددی نشان دادند که الگوریتم پیشنهادی راه حل بهینه را برای نمونه هایی به دست آورد که راه حلهای بهینه اثبات شده اند. به علاوه، جستجوی تابوی (ممنوعه) پیشنهادی ما بهترین راه حل معروف یافت شده در منابع و مراجع را پیدا کرد یا از لحاظ محاسبه ای بسیار کوتاه از آنها پیشی گرفت. این قابل توجه است که جستجوی ممنوعه پیشنهادی ما راه حلهای مشابه را در هر اجرا نسبت به روشهای دیگر پیشنهادی برای USAHLP به دست آورد. TS پیشنهادی ما دارای عملکرد بهتر نسبت به TS اخیرا پیشنهاد شده (سیلوا و کانها، 2009) از هر دو نظر مقادیر راه حل و زمان محاسبه ای می باشد.

برچسب‌ها: دانلود رایگان مقالات انگلیسی مهندسی فناوری اطلاعات IT، دانلود رایگان مقالات انگلیسی مهندسی کامپیوتر