Abstract
Power system stabilizers (PSSs) are the most well-known and effective tools to damp power system oscillation caused by disturbances. To gain a good transient response, the design methodology of the PSS is quite important. The present paper, discusses a new method for PSS design using the multi-objective optimization approach named Strength Pareto approach. Maximizations of the damping factor and the damping ratio of power system modes are taken as the goals or two objective functions, when designing the PSS parameters. The program generates a set of optimal parameters called Pareto set corresponding to each Pareto front, which is a set of optimal results for the objective functions. This provides an excellent negotiation opportunity for the system manager, manufacturer of the PSS and customers to pick out the desired PSS from a set of optimally designed PSSs. The proposed approach is implemented and examined in the system comprising a single machine connected to an infinite bus via a transmission line. This is also done for two familiar multi-machine systems named two-area four-machine system of Kundur and ten-machine 39-bus New England system. Parameters of the Conventional Power System Stabilizer (CPSS) are optimally designed by the proposed approach. Finally, a comparison with famous GAs is given.
1. Introduction
Ever increasing complexity of electric power systems has increased research interests in developing more suitable methodologies for power system stabilizers (PSSs). PSSs are the most effective devices for damping low frequency oscillations and increasing the stability margin of the power systems [1]. In fact, a PSS provides the excitation system with a proper supplementary signal in-phase with the rotor speed deviation resulting stable operation of the synchronous generator.
5. Conclusion
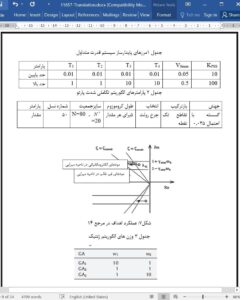
In the present paper, a novel method of CPSS design named Strength Pareto Evolutionary Algorithm (SPEA) is introduced. The SMIB, TAFM and New England are three well-known power systems used to exercise the PSS design methodology. Maximizing the minimum damping ratio and minimum damping factor of dominant oscillatory modes of the aforementioned systems are employed as two objectives while the PSS parameters are optimization variables. Moreover in the present paper, we have reached some optimum answers which seem to dominate GA results. The designer is free to select any of the results. However, the present paper could not zoom on the differences of Pareto fronts’ members very much, but recommends it for future works. Also the researchers may work on possible better objective functions.