Abstract
A numerical study on the free vibration analysis for laminated conical and cylindrical shell is presented. The analysis is carried out using Love's first approximation thin shell theory and solved using discrete singular convolution (DSC) method. Numerical results in free vibrations of laminated conical and cylindrical shells are presented graphically for different geometric and material parameters. Free vibrations of isotropic cylindrical shells and annular plates are treated as special cases. The effects of circumferential wave number, number of layers on frequencies characteristics are also discussed. The numerical results show that the present method is quite easy to implement, accurate and efficient for the problems considered.
1. Introduction
Laminated composite materials are increasingly used in aerospace, mechanical and civil engineering structures. With the increasing use of fiber-reinforced composites as structural elements, studies including the linear and nonlinear vibration of composite material shell are receiving considerable attention. This arises from the fact that, by taking advantage of its anisotropic material properties and light weight with high strength, the materials can be used very efficiently [2,32]. Because of the practical importance of the free vibration analysis of the composite laminated conical shell in structural, aerospace, nuclear, petrochemical, submarine hulls, and mechanical applications, a few investigators have made efforts to deal with free vibration analysis of this type of structures. Various methods for analyzing free vibrations of the conical shell such as the finite element method, Ritz method, Galerkin method, the other numerical approximate methods and the differential quadrature method have been tried. Unsymmetric free vibration of orthotropic sandwich shells of revolution has been made by Bacon and Bert [1].
5. Conclusions
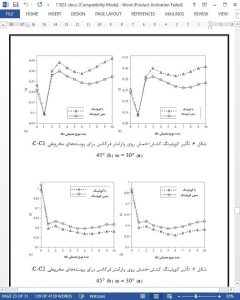
The numerical solution of partial differential equations plays a considerable role in the areas of engineering. Therefore, an effective numerical technique for the solution of partial equations is very desirable. In seeking a more efficient numerical method that requires fewer grid points yet achieves acceptable accuracy, the method of DSC was introduced by Wei [43].
The work presented here concerns the use of DSC method for the vibration analysis of laminated conical and cylindrical shells. Results were compared with existing solutions showing excellent performance. It is found that the convergence of DSC approach is very good and the results agree well with those obtained by other researchers. Thus, the DSC method provides an accurate, efficient means of solving problems for orthotropic laminated conical and cylindrical shells.