ترجمه مقاله ماتریس های مشتق گیری در پایه های چند جمله ای - نشریه اشپرینگر

قیمت خرید این محصول

۳۹,۰۰۰ تومان

دانلود رایگان نمونه دانلود مقاله انگلیسی

عنوان فارسی

ماتریس های مشتق گیری در پایه های چند جمله ای

عنوان انگلیسی

Differentiation matrices in polynomial bases

صفحات مقاله فارسی

16

صفحات مقاله انگلیسی

8

سال انتشار

2016

رفرنس

دارای رفرنس در داخل متن و انتهای مقاله

نشریه

اشپرینگر - Springer

فرمت مقاله انگلیسی

PDF

فرمت ترجمه مقاله

pdf و ورد تایپ شده با قابلیت ویرایش

فونت ترجمه مقاله

بی نازنین

سایز ترجمه مقاله

14

نوع مقاله

ISI

نوع نگارش

مقالات پژوهشی (تحقیقاتی)

نوع ارائه مقاله

ژورنال

شناسه ISSN مجله

2251-7456

کد محصول

5725

وضعیت ترجمه منابع داخل متن

به صورت عدد درج شده است ✓

وضعیت فرمولها و محاسبات در فایل ترجمه

به صورت عکس، درج شده است

ضمیمه

ندارد ☓

بیس

نیست ☓

مدل مفهومی

ندارد ☓

پرسشنامه

ندارد ☓

متغیر

ندارد ☓

رفرنس در ترجمه

در داخل متن و انتهای مقاله درج شده است

رشته های مرتبط با این مقاله

ریاضی

گرایش های مرتبط با این مقاله

ریاضی محض

مجله

علوم ریاضی - Mathematical Sciences

دانشگاه

بخش STEM، دانشکده هاوایی-ماوی، ایالات متحده آمریکا

کلمات کلیدی

الحاق چندجمله‌ای، پایه‌های چند جمله‌ای، مشتق‌گیری

کلمات کلیدی انگلیسی

Polynomial interpolation - Polynomial bases - Differentiation

doi یا شناسه دیجیتال

https://doi.org/10.1007/s40096-016-0177-x

فهرست مطالب

چکیده
مقدمه
پایه‌های درجه-مدرج
پایه‌های درجه-مدرج ویژه
پایه برنشتاین
پایه لاگرانژ
نکات نتیجه‌گیری

تصاویر فایل ورد ترجمه مقاله (جهت بزرگنمایی روی عکس کلیک نمایید)

نمونه چکیده متن اصلی انگلیسی

Abstract

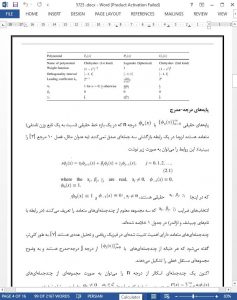
Explicit differentiation matrices in various polynomial bases are presented in this work. The idea is to avoid any change of basis in the process of polynomial differentiation. This article concerns both degree-graded polynomial bases such as orthogonal bases, and non-degree-graded polynomial bases including the Lagrange and Bernstein bases.

In this paper, we have found explicit formulas for the differentiation matrix, D, in various polynomial bases. The most important advantage of having D explicitly is that there is no need to go from one basis to another (normally monomial) to differentiate a polynomial in a given basis. Moreover, having D, we can easily find higher order derivatives of any polynomial in its original basis. One may hope that new and more efficient polynomial-related algorithms, such as root-finding methods, can be developed using D.

These results can be easily extended to matrix polynomials in different bases.

نمونه چکیده ترجمه متن فارسی

چکیده
ماتریس مشتق‌گیری صریح در چند پایه چند جمله‌ای در این مقاله ارائه شده‌ است. ایده این است که از هرگونه تغییر پایه در فرآیند مشتق‌گیری چند جمله‌ای اجتناب کنیم. این مقاله هم دارای پایه‌های چند جمله‌ای درجه - مدرج مانند پایه‌های متعامد، و هم دارای پایه‌های چند جمله‌ای غیر مدج شامل پایه‌های لاگرانژ و برنشتاین است.
در این مقاله، فرمول‌های صریحی را برای ماتریس مشتق‌گیری D در پایه‌های چندجمله‌ای مختلف به دست آورده‌ایم. مهمترین مزیت داشتنِ صریح D این است که هیچ نیاز به رفتن از پایه‌ای به پایه دیگر (معمولا تک جمله‌ای) برای مشتق‌گیری از یک چندجمله‌ای در پایه ارائه شده نیست. علاوه‌براین، با داشتن D می‌توانیم به سادگی مشتقات مرتبه بالاتر یک چندجمله‌ای را در پایه اصلی آن بیابیم. می‌توان امیدوار بود که الگوریتم‌های کارامدتر مربوط به چندجمله‌ای، مانند روش‌های ریشه‌یابی، را بتوان با استفاده از D توسعه داد.
این نتایج را می‌توان به سادگی به چندجمله‌ای‌های ماتریسی در پایه‌های مختلف توسعه داد.

برچسب‌ها: دانلود رایگان مقالات انگلیسی ریاضی و آمار