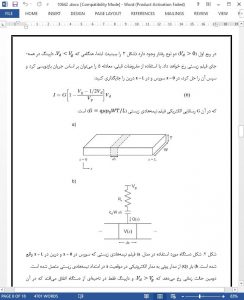
In recent years, organic electrochemical transistors (OECTs) have emerged as attractive devices for a variety of applications, particularly in the area of sensing. While the electrical characteristics of OECTs are analogous to those of conventional organic field effect transistors, appropriate models for OECTs have not yet been developed. In particular, little is known about the transient characteristics of OECTs, which are determined by a complex interplay between ionic and electronic motion. In this paper a simple model is presented that reproduces the steady-state and transient response of OECTs by considering these devices in terms of an ionic and an electronic circuit. A simple analytical expression is derived that can be used to fit steady-state OECT characteristics. For the transient regime, comparison with experimental data allowed an estimation of the hole mobility in poly(3,4-ethylenedioxythiophene) doped with poly(styrene sulfonate). This work paves the way for rational optimization of OECTs.
1. Introduction
The field of organic electronics has grown significantly in the past 20 years largely due to the many desirable properties of organic semiconductors such as low cost, ease of processing and tunability through synthetic chemistry.[1] Among organic semiconductor devices, organic thin film transistors (OTFTs) have attracted considerable interest for their application in printed electronics.[2] Within the subset of OTFTs, organic electrochemical transistors (OECTs) have distinguished themselves in recent years given their simple fabrication and low voltage operation.[3] The ability to operate in aqueous environments and the integration with microfluidics make OECTs excellent candidates for a variety of applications, especially in the area of sensing.[4]
3. Conclusions
In this paper we have presented a model that describes the steady-state and transient behavior of OECTs. Utilizing a two circuit approach, the ionic and electronic nature of OECTs was accounted for and realistic device behavior was reproduced. The model showed excellent agreement when used to fit typical device behavior at steady-state. The source-drain current transient was predicted to exhibit two types of characteristic behavior: monotonic decay or spike-and-recovery. Both types of response were demonstrated in a PEDOT:PSS OECT by variation of the drain voltage. The model shows how tuning of the appropriate device parameters can be used as a means to minimize the response time of OECTs. Typical materials parameters extracted from comparison with experiment were reasonable estimates for the mobility of PEDOT:PSS. In general, this simple model is a powerful tool for design of OECTs, which can be modified to account for many variations in device design.