Ambulance location problem is a key issue in Emergency Medical Service (EMS) system, which is to determine where to locate ambulances such that the emergency calls can be responded efciently. Most related researches focus on deterministic problems or assume that the probability distribution of demand can be estimated. In practice, however, it is difcult to obtain perfect information on probability distribution. Tis paper investigates the ambulance location problem with partial demand information; i.e., only the mean and covariance matrix of the demands are known. Te problem consists of determining base locations and the employment of ambulances, to minimize the total cost. A new distribution-free chance constrained model is proposed. Ten two approximated mixed integer programming (MIP) formulations are developed to solve it. Finally, numerical experiments on benchmarks (Nickel et al., 2016) and 120 randomly generated instances are conducted, and computational results show that our proposed two formulations can ensure a high service level in a short time. Specifcally, the second formulation takes less cost while guaranteeing an appropriate service level.
1. Introduction
Te design of Emergency Medical Service (EMS) systems that afects people’s health and life focuses on how to respond to emergencies rapidly. Ambulance location problem is one of the key problems in EMS system, which mainly consists of determining where to locate bases, also named as emergency service facilities, and the employment of ambulances in order to serve emergencies efciently and to guarantee patient survivability. Tere have been various researches investigating ambulance location problem (e.g., [1, 2]) since it is introduced by Toregas et al. (1974).
6. Conclusion
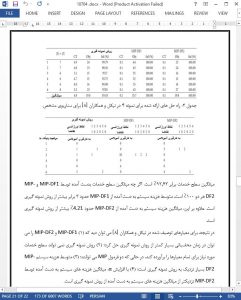
Tis paper investigates an ambulance location problem with ambiguity set of demand, in which the probability distribution of the uncertain demand is unknown. In such a datadriven environment, only the mean and covariance demands at emergency points are known. Te problem is to determine the base locations and the number of ambulances at each base, aiming at minimizing the total cost associated with locating bases and assigning ambulances. We propose a distribution-free model with chance constraints. Ten two approximated MIP formulations with diferent approximation methods of chance constraints are proposed, which are based on diferent ambiguity sets of the unknown probability distribution. Numerical experiments on benchmarks and 120 randomly generated instances are conducted, and the computational results show that the frst approximated MIP formulation is much conservative with overhigh system cost, while the second approximated MIP formulation is more cost saving with service level appropriately ensured.