Abstract
The freezing point is one of the most critical properties required to complete the mathematical formulation related to the transport phenomena involved in the immersion chilling and freezing (ICF) of foods. Unfortunately, data for ternary and higher order systems are scarce. The aim of this work was to verify the validity of an excess Gibbs energy model for predicting the freezing point of multicomponent mixtures of electrolytes and non-electrolytes, considering the processing conditions used in immersion chilling and freezing of foods. The extended UNIQUAC model was used. Data obtained from literature corresponding to freezing points of the ternary systems: NaCl–KCl–H2O, NaCl–CaCl2–H2O, NaCl–MgCl2–H2O and NaCl–EtOH–H2O, were compared with predicted values. The model accuracy was satisfactory, the highest absolute deviation being smaller than 1.71 °C for the 378 data compared.
1. Introduction
Immersion chilling and freezing (ICF) consist of soaking foods in a low freezing point liquid medium maintained at a low temperature. A number of economical and technical advantages over the conventional food chilling and freezing methods have been reported for the application of these refrigerating media: (1) high heat transfer rates with small temperature gradients, (2) fine ice crystal structure in foods is ensured, (3) the product surface freezes immediately in a solid crust that limits the osmotic transfer and gives an excellent appearance, (4) the operation is easy to maintain, convenient for automation and the labor costs are substantially reduced, and (5) the technology is environmentally friendly (Fikiin and Fikiin, 1998; Fikiin, 2003). Industrially, the ICF process has been used extensively for chilling or freezing fish (shrimp, crab, sardines, tuna, etc.) in brine (sodium chloride or even calcium chloride). Various products and processing conditions for binary and ternary aqueous solutions can be found in the literature. For example, diced carrots, sweet corn, beans and peas were frozen in a NaCl– glucose–H2O solution; and haddock, salmon and tuna were frozen in a NaCl–CaCl2–KCl–H2O solution (Lucas and Raoult-Wack, 1998).
5. Conclusions
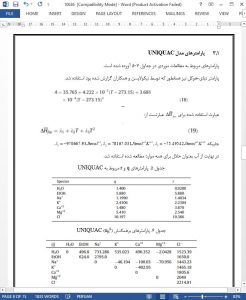
The extended UNIQUAC model was adequate for predicting the freezing point in multicomponent systems related to the cooling and/or freezing by immersion. A satisfactory accuracy was observed for the systems studied. The model may be used to explore different scenarios where at present there is a lack of experimental and theoretical data.