Abstract

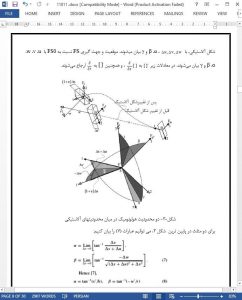
Using Hamilton’s principle the coupled nonlinear partial differential motion equations of a flying 3D Euler–Bernoulli beam are derived. Stress is treated three dimensionally regardless of in-plane and out-ofplane warpings of cross-section. Tension, compression, twisting, and spatial deflections are nonlinearly coupled to each other. The flying support of the beam has three translational and three rotational degrees of freedom. The beam is made of a linearly elastic isotropic material and is dynamically modeled much more accurately than a nonlinear 3D Euler–Bernoulli beam. The accuracy is caused by two new elastic terms that are lost in the conventional nonlinear 3D Euler–Bernoulli beam theory by differentiation from the approximated strain field regarding negligible elastic orientation of crosssectional frame. In this paper, the exact strain field concerning considerable elastic orientation of crosssectional frame is used as a source in differentiations although the orientation of cross-section is negligible.

1 Introduction

Beams are one of the most important structural elements in engineering fields. To provide the structure with less weight makes designer choose more flexible beams. As the flexibility of the beam increases, its dynamic modeling becomes more complicated in return.

Karray et al. [1] have treated the two flexible links of space-based flexible manipulator as Euler–Bernoulli beams, free to deform transversely in the orbital plane. Hiller [2] has considered only three elastic degrees of freedom for each link as an Euler–Bernoulli beam. Shi et al. [3] have modeled a planar flexible link by an Euler–Bernoulli beam. Chen [4] has presented a linearized dynamic model for multilink planar flexible manipulators which can include an arbitrary number of flexible links. 9

Conclusions

Nonlinear partial differential equations of motion of a 3D Euler–Bernoulli beam with six-DOF flying support are exposed. The beam experiences compression, tension, torsion, and two spatial bendings elastically while negligible elastic orientation is produced in its crosssectional frame. The motion equations involve two new elastic terms that had been lost in the traditional nonlinear 3D Euler–Bernoulli beam theory by differentiation from the approximated strain field regarding negligible elastic orientation of cross-sectional frame. The differentiation should have been derived from the exact strain field concerning large elastic orientation of the crosssectional frame. These two elastic terms have given the resulting motion equations a higher accuracy than that of the nonlinear 3D Euler–Bernoulli beam theory. They account for the enhancement of the nonlinear 3D Euler–Bernoulli beam theory.