Abstract
This paper proposes a novel multi-scale approach for the reliability analysis of composite structures that accounts for both microscopic and macroscopic uncertainties, such as constituent material properties and ply angle. The stochastic structural responses, which establish the relationship between structural responses and random variables, are achieved using a stochastic multi-scale finite element method, which integrates computational homogenisation with the stochastic finite element method. This is further combined with the first- and second-order reliability methods to create a unique reliability analysis framework. To assess this approach, the deterministic computational homogenisation method is combined with the Monte Carlo method as an alternative reliability method. Numerical examples are used to demonstrate the capability of the proposed method in measuring the safety of composite structures. The paper shows that it provides estimates very close to those from Monte Carlo method, but is significantly more efficient in terms of computational time. It is advocated that this new method can be a fundamental element in the development of stochastic multi-scale design methods for composite structures.
1. Introduction
Typical composite components are laminates comprising layers of fibre reinforced composite laminae, each of which are made of fibres embedded in matrix. The assembly of the fibres and matrix materials to create a lamina, as well as the lay up and curing of laminae, is a complicated process and may involve a lot of uncertainty. Therefore, the material properties of a composite laminate are random in nature. Sources of significant uncertainty include: variations in volume fractions of fibre and matrix, voids in the matrix and between fibres and matrix, imperfect bonding between constituents, cracks, fibre damage, random and/or contiguously packed fibres, misaligned fibres, temperature effects, non-uniform curing of the matrix material, residual stresses, etc. Uncertainties in these factors propagate to a larger scale and are reflected in variability of the stiffness and strength that characterise the overall structural behaviour [1–7]. Consequently, high safety factors of the order of 8–10 [8] are introduced in current deterministic based structural design, thereby not taking full advantage of composite materials. These issues may be addressed in a probability based design context [9–11] equivalent to Eurocode, for example.
5. Conclusions
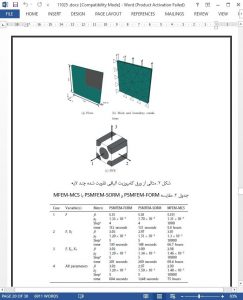
In this paper, a multi-scale finite element based reliability analysis method is proposed for composite structures. The proposed method enables both microscopic uncertainties, such as those in constituent material properties, and macroscopic uncertainties, such as ply orientation angles, to be taken into account. The new reliability analysis framework (PSMFEMFORM and PSMFEM-SORM) couples a recently developed perturbation-based stochastic multi-scale finite element method with the first- and second-order reliability methods. Formulations of the stochastic homogenization method and its finite element implementation are described. Procedure to perform the proposed multi-scale finite element based reliability analysis methods is thoroughly introduced. In addition, Monte Carlo simulation has been coupled with the deterministic multi-scale finite element method to form the MFEM-MCS to evaluate the performance of PSMFEM-FORM and PSMFEM-SORM.