Abstract
In this paper a nonlinear model is presented to demonstrate the relation between production and marketing departments. By introducing some functions such as pricing cost and market share loss functions it will be tried to show some aspects of market modelling which has not been regarded before. The proposed model will be a constrained signomial geometric programming model. For model solving, after variables’ modifications an iterative technique based on the concept of geometric mean will be introduced to solve the resulting non-standard posynomial model which can be applied to a wide variety of models in non-standard posynomial geometric programming form. At the end a numerical analysis will be presented to accredit the validity of the mentioned model.
I. INTRODUCTION
IN traditional production and lot sizing models, demand and variable productions cost are assumed to be constant, while it is not the same in real world. In the past few years, models attempting to link production and marketing decisions, have been proposed to determine an item’s price, lot size and marketing expenditure per unit simultaneously. Production and marketing departments are two highly interdependent units of all the firms. Decisions of one department frequently influence the performance and decision of the other. For instance the information presented by marketing department can be used as a basis for production department to set its production planning. On the other hand, information such as capacity constraint or degree of flexibility from production department can influence the marketing department performance [1].
V. CONCLUSION
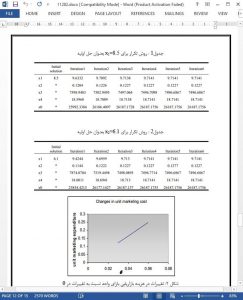
This paper formulated a comprehensive previously unexplored model regarding market share loss and pricing cost functions to demonstrate the relation between two important managerial departments of production and marketing. As the model was in signomial form, it was needed to change that to standard posynomial form. In order to do this change, the concepts behind the relations between geometric and arithmetic means have been applied. After transformation, as the dual program was a parametric equation system, an efficient iterative algorithm is used to solve the resulting model. Considering the given numerical example the model is analyzed and investigated for the effect of changes in parameters on decision variables. The analysis of the model could approve the validity of the proposed model. This study provides a rather comprehensive framework for joint pricing and lot sizing decisions, and can be easily expanded to investigating multi- product firms using the mentioned techniques.