Abstract
In this study, the traditional Markov chain method for wind speed modeling is analyzed and two improvements are introduced. New states categorization step and wind speeds simulation step are presented. They both take advantage of the empirical cumulative distribution function of the wind speed time series. Performances of the new method are tested in terms of modeling and short-term forecasting. The results suggest that this method overperforms the traditional one for modeling.
1. Introduction
Wind characteristics are important for the evaluation of wind resources, performance of wind turbines and their power production. Due to the fact that the Weibull distribution has been unable to represent all the wind regimes encountered in nature, researchers have continued to propose new wind speed probability models (see Ref. [1] for a review).
The Markov chain method is used in numerous studies for modeling various types of wind speed time series [2e7] (see also Refs. [8,9] in the multivariate setting). The procedure for solving such problems using the Markov chain modeling method is relatively clear. Firstly, all of the values of a time series are distributed into several states. Secondly, supposing the series of states is ruled by a homogeneous Markov chain, a transition probability matrix of these states is estimated. Thirdly, this matrix is used to generate a new series of states. Fourth, each state in this new series is converted into a wind speed value with a certain random generator. The final product is a synthetic time series generated from the observed series, with faithfully reproduced statistical parameters.
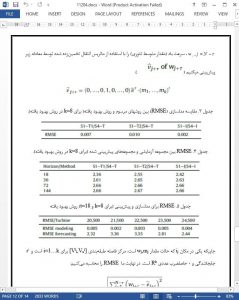
5. Conclusion
In this study, the application of the traditional Markov chain method for wind speed modeling is analyzed. The first step which is the state categorization might generate a huge and inefficient transition probability matrix.
Moreover, the wind speeds generation from the states simulation in the fourth step might not reproduce some statistical features and stylized facts observed in the data (bimodal distribution, Weibull tails, etc.).